17x17: some Simulated Annealing updates

Note: this is part of a series of posts is related to the “17x17 Challenge” posted by Bill Gasarch. The goal is to color cells of a 17 by 17 grid, using only four colors, such that no rectangle is formed from four cells of the same color.

Just a few follow-ups to my previous post in which I use a simulated annealing-type algorithm to find a good (hopefully complete) cover of a grid by swapping rows and columns from four identical sub-grids of 74 colors.

Easing into new thresholds

I modified my algorithm so that the likelihood of jumping into the highest permitted energy level is decreased over time; thus instead of having an abrupt transition to a new threshold, resulting in a steep dive, we instead ease into the new energy level.

Here is a graph of a run with the adjusted meta-heuristic (in blue) alongside a previous abrupt threshold transition run (in black). You can check compare it to the graph from the previous post:

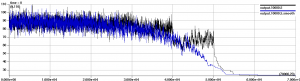
a more smooth graph vs. a graph with abrupt changes at each threshold change

Unfortunately this change didn’t cause any improvement in the solutions generated. They still seem to flatten at a grid with 19 - 22 uncolored cells.

Testing a combination of sub-grids with known good solution

I wondered if the lower bound I was smacking into was caused by the fact that I was trying to find a combination of four permutations of the same subset, and perhaps this particular subset didn’t mesh all that well with itself.

In the original blog posting laying out this challenge there is four-coloring of 17x17 with only one cell left un-colorable in a truly painful refactoring process, I modified my script to take four separate and distinct sub-grids and perform the same shuffling procedure.

Rather than find the original arrangement of the colored subsets or one nearly as good, the program settles on a solution with around 30 uncolored cells. That is worse than my original version, corresponding to the fact that there are fewer cells to work with in this latter set of colored subsets: 288 vs. 296.

Conclusion

This doesn’t say anything about whether a full-cover can likely be obtained by permuting four overlapping copies of a single subset of colors. It does tell us that either my code is flawed, this isn’t a particularly effective method for this kind of search, or it needs to be tuned better.