Parallel List Comprehensions with a Monte Carlo example

GHC has an extension to the list comprehensions syntax that replicates the functionality of zipWith, by allowing you to have two generators running in parallel. Turn on the extension in GHCi like so:

Prelude> :set -XParallelListComp

I use the extension below to generate an infinite list of random coordinates (scaled to a  1000x1000 grid) using two different  Linear Congruential Generators running in parallel. It should be simple to modify the code below to actually run the generators concurrently using Data Parallel Haskell (although I haven’t had a chance to play with that yet).

randPoints :: (Integral i) => i -> [(i,i)]
randPoints s = drop 1 [ (scale x, scale y) | x <- g1 | y <- g2 ]
    where -- two Linear Congruential Generators (from Borland C, glibc):
        g1 = s : [ (g*22695477 + 1) `mod` 2^32 | g <- g1]
        g2 = s : [ (g*1103515245 + 12345) `mod` 2^32 | g <- g2]

-- adjust the random output to fit a 1000x1000 plane:  
scale v = (v `mod` 1000) - 500

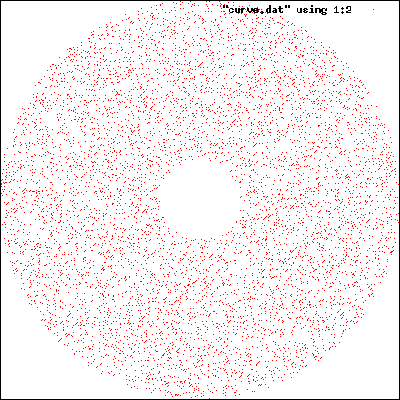
Then we can use another list comprehension, this time with boolean guards, to generate random points that lie within an outer circle (and outside an inner circle):

monteDonut = [p | p@(x,y) <- randPoints 42, let b= x^2+y^2, b<500^2, b>10000]

Finally from GHCi we can use the Gnuplot library to easily plot the points we generated:

*Main> :m + Graphics.Gnuplot.Simple 
*Main> plotDots [Aspect(Ratio 1), XTicks Nothing, YTicks Nothing] (take 10000 monteDonut) 

…and we get a nice Monte Carlo donut with sprinkles!: